|
Hier sind sämtliche Kommentare zu finden, in chronologischer Reihenfolge. Dies ist Seite 172 von 557. (20 Kommentare pro Seite bei 11130 Wortmeldungen insgesamt.)
eltom, 16.10.2006 16:03 MEZ
ad Google-Weisheiten hehe
R.U.GAY, 16.10.2006 12:44 MEZ
ad schedule : 42. Kalenderwoche 2006 Ois guade, es zwoa rotz'n. De woch werd's woi de 5k-grenze schoff'n...
eltom, 16.10.2006 11:37 MEZ
ad Nachtrag: Heidelberg SOOOOOOOOUUUL CALIBURRRRRRRRRRRRRRRRRRRRRR
R.U.GAY, 16.10.2006 10:14 MEZ, ad op.cit. Alles Gute griff und eltom...ihr seid herzlichst eingeladen wieder nach HDB zu kommen...Siegfried...
Gü, 16.10.2006 9:33 MEZ
ad IE7 soll kommen... Ich find das witzig: noch bevor er herauskommt, gibt es erste Tips, wie man die Installation vermeiden kann...
Jano Nym, 15.10.2006 17:35 MEZ, ad op.cit. Mecht gar ned wissen, wia vü se des kosten wead!
mag.e, 14.10.2006 19:59 MEZ, ad op.cit. Schon frech...
BLP, 13.10.2006 21:28 MEZ
ad people : sym Ja, was hält er denn da in seinem Händchen?
der Käptn, Junge!, 13.10.2006 15:43 MEZ
ad Der Kopf der Woche, 28.8.2006 Ich bitte bei der gängigen und verständlichen Terminologie zu bleiben:
Kopf = Kopp
also, Nagel am Kopp:
"Der Kopp der Woche, 28.8.2006"
Ausserdem fällt in letzter Zeit auffälligerweise das Fehlen vieler wichtiger, dem Verständnis nur zuträglichen, verstärkenden Niveau-Ausdrücken wie "Junge, Schisser, echt jetzt, usw" stark negativ auf.
Die momentane Schreibe raff ich auf alle Fälle überhaupt ned, scheisse ned nomal, echt jetzt ihr Nassbirnen! Oder wollt ihr sagen, dass ich blöd bin, ein Vollspasti oda wat?!?
schwarzerkaffee, 12.10.2006 13:51 MEZ, ad op.cit. aja / statt \
das haben meine 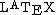 Fingerchen automatisch gemacht. Fingerchen automatisch gemacht.
schwarzerkaffee, 12.10.2006 13:44 MEZ
ad 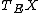 rulez! rulez! [ tex ] x_1^n = x_2^n + x_3^n [/ tex ]
mhhh...
schwarzerkaffee, 12.10.2006 12:16 MEZ
ad Der Kopf der Woche, 28.8.2006 ohne Frage.
koala, 12.10.2006 11:56 MEZ, ad op.cit. Aber fesch ist sie trotzdem.
griff, 12.10.2006 10:23 MEZ, ad op.cit. @schwarzerkaffe: so klappts auch mitm nachbarn... hab ich ja jestern jesagt, dat dass  sein muss... :) sein muss... :)
mag.e, 12.10.2006 10:22 MEZ, ad op.cit. Jetzt war griff schneller...ich wollte auch gerade.
griff, 12.10.2006 10:22 MEZ, ad op.cit. 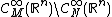
wobei die {\it moderaten Funktionen} 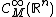 definiert sind als die Menge aller glatten, positiven Funktionen definiert sind als die Menge aller glatten, positiven Funktionen 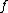 auf auf 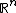 sodass für alle Kompakta sodass für alle Kompakta 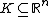 und alle Multiindices und alle Multiindices  für die es positive Zahlen für die es positive Zahlen 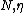 und und  existieren sodass für alle existieren sodass für alle 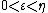 gilt: gilt:
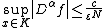
Die Menge der {\it vernachlaessigbaren Funktionen} 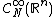 ist ebenso definiert, nur fordern wir fuer {\it alle } ist ebenso definiert, nur fordern wir fuer {\it alle } 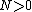 dass dass
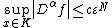
schwarzerkaffee, 11.10.2006 23:17 MEZ, ad op.cit. Also es ist so. Es ist ja bekanntlich so dass man (Schwartz) Distributionen schlecht multiplizieren kann. Ich möchte beinahe behaupten dass die Theorie der Distributionsprodukte fast so reichhaltig ist wie die Theorie der
invertierbaren Matrizen mit Determinante 0. Der werte Herr Colombeau hat sich dazu herabgelassen auf unserem ärmlichen Institut einen
Kolloquiumsvortrag zu halten (Im Nachhinein gesehen - da ich nun weiß dass Räume nach diesem Mann benannt sind - kommen mir die Fragen und Einwürfe der hiesigen Mathematikbelegschaft recht ärmlich vor). Das war sehr lustig. Dieser Typ sprach natürlich ein sehr liebenswertes Frankoangelsächsisch und plauderte etwas aus dem Nähkästchen, etwa berichtete er von Gesprächen
mit Herrn Schwartz über Distributionen und dergleichen. Überdies verbreitet er einen dezent geheimnisvollen Nimbus, da er uns Ergebnisse vorenthielt, da sie militärischer Natur waren (es ging um Projektile die auf Panzer abgefeuert werden, die Aussenhaut durchdringen und im Innenraum ein kleines Sodom und Gomorra vom Zaun zu reissen). Die Grundidee ist wie folgt:
Die Colombeau Algebra ist definiert als
[ tex ] \mathcal{C}^\infty_M(\mathbb{R}^n)\backslash
\mathcal{C}^infty_N(\mathbb{R}^n) [\ tex ]
wobei die {\it moderaten Funktionen} [ tex ] \mathcal{C}^\infty_M(\mathbb{R}^n) [\tex] definiert sind als die Menge aller glatten, positiven Funktionen [tex] f [\text] auf [tex] \mathbb{R}^n [\tex] sodass für alle Kompakta [tex]K\subseteq\mathbb{R}^n[\tex] und alle Multiindices [tex]\alpha[\alpha] für die es positive Zahlen [tex] N, \eta[\tex] und [tex] c[\tex] existieren sodass für alle [tex}0<\varepsilon<\eta[tex] gilt:
[tex] \sup_{x\in K} \left|D^alpha f\right|\leq \frac{c}{\varepsilon^N}
[\tex]
Die Menge der {\it vernachlaessigbaren Funktionen} [tex] \mathcal{C}^infty_N(\mathbb{R}^n) [\ tex ] ist ebenso definiert, nur fordern wir fuer {\it alle } [tex] N > 0 [\tex] dass
[tex] \sup_{x\in K} \left|D^alpha f\right|\leq c \varepsilon^N [\tex]
Das dieses Ding auch eine Algebra ist, d.h. dass man Colombeau Distributionen multiplizieren kann, dass waere wieder einmal beyond the scope of this text. Lest selbst etwa in arXiv:gr-qc/9610017v1. Gute Nacht.
monz.tar.bz2, 11.10.2006 21:41 MEZ, ad op.cit. kann jo lei a mathematika sein, dea von
"Frau" iba " Feuchtigkeitsabsonderung" auf "Pflanze" kimmt
roli, 11.10.2006 19:12 MEZ, ad op.cit. Bevor der Ruf des Blogs komplett den Bach runter geht, könnte ja jemand noch etwas Sinnvolles zu Räumen vom Colombeau Typ sagen. Ich muss jetzt leider weg, sonst würde ich das natürlich übernehmen.
mag.e, 11.10.2006 18:24 MEZ, ad op.cit. Ist schon faszinierend, wofür man Algebra alles verwenden kann.
|
