|
dr.e,
27.9.2005 11:53 MEZ

"Ist die Trägheit eines Körpers von dessen Energieinhalt abhängig?" fragte genau vor 100 Jahren Albert Einstein in den Annalen der Physik 18, p. 639-643. Wer einen ehrfürchtigen Blick auf die Werk des Meisters werfen will, der kann ihn entweder hier auf das Bild im Blog richten oder sich das Faksimile ausdrucken, einrahmen und über den Hausaltar hängen:
http://www.physik.uni-augsburg.de/annalen/history/[...]
Lasst uns also heute einen Moment in der Forschung innehalten und uns an diesen denkwürdigen Augenblick erinnern, als vor 100 Jahren eine Formel niedergelegt wurde die heute in der Form 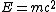 ein jeder kennt und sogar ohne zu zögern zitiert. Im Missbrauch nur von Heisenbergs ein jeder kennt und sogar ohne zu zögern zitiert. Im Missbrauch nur von Heisenbergs 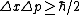 übertroffen, kann sie doch ohne Übertreibung als die Formel angesehen werden, welche die Weltöffentlichkeit quasi mit dem Mysterium der Physik identifiziert. Und das, wo sie doch nur eine lächerliche Multiplikation und ein Quadrat beinhaltet. Keine partielle Ableitung, ein Limes, eine Gauss-Klammer, ein komplexes Konturintegral, ein schickes übertroffen, kann sie doch ohne Übertreibung als die Formel angesehen werden, welche die Weltöffentlichkeit quasi mit dem Mysterium der Physik identifiziert. Und das, wo sie doch nur eine lächerliche Multiplikation und ein Quadrat beinhaltet. Keine partielle Ableitung, ein Limes, eine Gauss-Klammer, ein komplexes Konturintegral, ein schickes 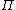 , Tensor- oder Skalarprodukte, Bessel- oder Hankel-Funktionen, Operatoren auf Hilberträumen, Quaternionen, eine Lie-Klammer, ja nichtmal eine Wurzel! , Tensor- oder Skalarprodukte, Bessel- oder Hankel-Funktionen, Operatoren auf Hilberträumen, Quaternionen, eine Lie-Klammer, ja nichtmal eine Wurzel!
mag.e, 29.9.2005 11:30 MEZ [ tex ] ... [/ tex ] statt $ ... $
schwarzerkaffee, 29.9.2005 10:13 MEZ einmal hat mir ein netter herr beim kaffeeautomat im vfh etwas von $\frac{v^4}{c^4}$ erklärt und vom zeichen mohammends berichtet etc. ich seh schon ....
Guter Physiker, 29.9.2005 9:48 MEZ Und als guter Physiker erhält man 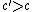 . .
MovGP0, 29.9.2005 2:18 MEZ Da fehlt doch noch was:
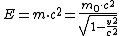
Man braucht also nur die Ruhemasse berücksichtigen, dann hat man auch eine nette Wurzel, jetzt nur noch die Geschwindigkeit differenzieren.
Natürlich muss man ja auch die gausche Verteilung der relativen Masse im Raum - ausgelöst durch die Brownschen Teilchenbewegungen berücksichtigen. Und dann muss man noch die Unschärferelation anwenden, da man Position und Masse nicht richtig bestimmen kann und sich somit ein Fehler ergibt. Und dann muss man noch...
gü, 27.9.2005 18:25 MEZ Die Formel ist ja gerade deswegen so bekannt, WEIL sie so einfach ist (d.h. einfach hinzuschreiben). Das mit dem Verstehen lass ich mal offen...
R.U.GAY, 27.9.2005 12:22 MEZ Na...of se wordklouver...
mag.e, 27.9.2005 12:17 MEZ The Return Of The Sprachreiniger?
wortklauber, 27.9.2005 12:13 MEZ also dass da keine partielle ableitung und keine wurzel drinstehen kann ich bestätigen, aber ich find weder eine Hankelfunktion, eine Lie-Klammer, einen Tensor (was ist das überhaupt?) oder ein komlexes Konturintegral.
mag.e, 27.9.2005 11:55 MEZ Wenigstens das mit der Wurzel lässt sich aber ändern:
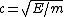
<< zurück
|
